Sobre el caos (I)

La visita de Buttercup en su forma décimo séptima me ha hecho retomar el interés por un tema fascinante: el caos. Si visitáis su blog comprenderéis por qué. Entre otros guiños, el lema de su fondo es “Lady in fractal”. Si consigo captar vuestro interés, en éste y otros artículos intentaré explicaros términos como atractor extraño, fractal, o efecto mariposa.
Hace algunos años la teoría del caos estuvo de moda. Recordaréis al matemático de Parque Jurásico explicar la teoría con el ejemplo de la gota sobre la mano. ¿Hacia dónde irá la gota? La teoría se aplicaba después de una forma simplona para explicar porqué no se pueden tener dinosaurios en un parque sin que surja el caos. Corramos un tupido velo…
Después de esta introducción cuyo único propósito es evitar que paséis sin más trámite al siguiente blog de vuestra lista, qué mejor manera para empezar que por el principio. No es redundancia:
“¿Qué había antes de que existiera el mundo tal como lo conocemos? Los griegos contestaron a esta pregunta mediante unos relatos y unos mitos.
Al principio, sólo existía el Vacío; los griegos lo llamaron Caos. ¿Qué es el Caos? Una inmensidad vacua, negra y oscura, en la que nada se veía. Una especie de caída, de vértigo, de confusión, sin fin, sin fondo. Era un vacío tan impresionante como una inmensa boca siempre abierta en la que todo quedara engullido en una misma noche indiferenciada.” Jean-Pierre Vernant, El universo, los dioses, los hombres.

Todos tenemos una idea bastante clara de lo que significa caos en el lenguaje común. Estuve a punto de iniciar esta serie de artículos como una de mis palabras de la semana, pero deseché la idea porque casi todos hubierais respondido sin dudar: caos es desorden.
Esto es cierto, pero hemos de diferenciar el concepto común de caos y el concepto matemático de caos. Dicho de otra manera, no todo lo que parece caótico, lo es en el sentido matemático. Pondré algunos ejemplos típicos. Si escuchamos los sonidos de claxon que genera una cola de cabreados conductores en un atasco, nos puede parecer que es un ejemplo de caos. Bueno, pues no. La distribución de pitidos frente al tiempo es aleatoria. No hay ninguna ley matemática que nos permitiera predecir cuándo se producirá el siguiente pitido. Es ruido (en sentido común y en sentido matemático).
Lo sorprendente de un fenómeno caótico es que sí obedece a unas leyes preestablecidas. A pesar de ello, su comportamiento les hace difícil de predecir. El paradigma es el tiempo meteorológico. Conocemos bastante bien la física de los fluidos. ¿Porqué es tan difícil acertar si lloverá el fin de semana? Algunos podríais contestar que la atmósfera terrestre es demasiado grande, demasiado compleja de modelizar. Estarías en lo cierto sólo en parte. La naturaleza caótica de los fenómenos no es una consecuencia de la complejidad de los mismos, sino que proviene de la propia naturaleza de las ecuaciones que los rigen. Hay sistemas caóticos que surgen de un simple sistema de tres ecuaciones.
Si conociéramos con absoluta precisión el estado inicial y las ecuaciones de un sistema caótico, seríamos capaces de predecir su evolución. Sin embargo, si cometiéramos un pequeño error en la medición de dicho estado inicial, la predicción se haría cada vez más inexacta, hasta el punto de no parecerse nada a la realidad. Es por eso que es tan difícil predecir el tiempo, porque es imposible conocer las temperaturas y presiones de todos los puntos del planeta en un momento dado. Sólo tenemos aproximaciones, y eso es lo que obtenemos con los grandes ordenadores de los institutos meteorológicos: aproximaciones.
De ahí el tan conocido efecto mariposa. El aleteo de una mariposa en Tailandia puede desencadenar un huracán en el Caribe. Si obviamos la evidente exageración, lo que nos quiere expresar esta frase es que pequeñas variaciones en las condiciones iniciales de un sistema caótico pueden producir efectos muy grandes en su evolución.
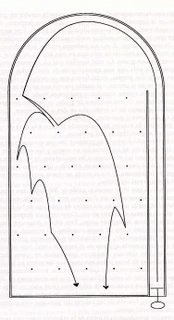
Otro ejemplo. Tomaré el que usa Edward N. Lorenz en su libro “La esencia del caos”. Imaginaos una máquina de pinball, pero que en lugar de dianas y demás, tiene pivotes regularmente distribuidos, representados en la siguiente figura como puntos. Si lanzamos dos veces una bola, es poco probable que la trayectoria se repita exactamente. Las pequeñas diferencias en la fuerza con la que lanzamos la bola se amplifican enormemente en los sucesivos rebotes. En teoría, conocemos perfectamente las ecuaciones que rigen el movimiento de la bola, los coeficientes de rozamiento, etc., pero si no tenemos absoluta precisión en la medición de la velocidad inicial de la bola, nuestra predicción de por dónde saldrá la bola será basura.

Terminaré este primer artículo recapitulando una primera definición de sistemas caóticos. Son aquellos que parecen aleatorios, a pesar de obedecer a unas leyes deterministas, debido a que son extremadamente sensibles a las condiciones iniciales.
Si os interesa, en próximos artículos veremos más características de estos fascinantes fenómenos.

Imágenes: Atractor de Lorenz en 3D y fractal realizado a partir de bolas navideñas, por Paul Bourke.