Sobre el caos (II)

Me temo que en el capítulo de hoy voy a tener que meterme en algunas honduras y nicaraguas, así que intentaré hacer el trago menos largo y duro (¡tócame el trago!), para que los legos y los tentes en la materia pillen algo (cacho no, lo siento, para eso ir al blog de Margarita la calentona).
Empezaré por hablaros de los sistemas dinámicos. No, no se tratan del conjunto de lamparita y cachivache que se colocan en las bicis para que den luz (perdón, suplico perdón). De una forma rápida, un sistema dinámico es cualquier porción del universo cuya evolución en el tiempo es determinista. ¿Cómo?¿Que qué co…píííí significa eso? Significa que existe una ley (antitabaco no, matemática) que determina lo que le va a pasar a continuación. Un ejemplo: un péndulo en movimiento. Si fuéramos unos tipos con la frente amplia y despejada, que no es mi caso, seríamos capaces de escribir una simple (o complicada) ecuación que describiera la posición angular de la pesa en un momento del tiempo t, determinado. Algo así como x'=f(x,t). También vale si hay algo de aleatoriedad, pero sólo un poquito, no más.
Básicamente, cualquier cosa puede ser un sistema dinámico. Lo único que hace falta es que seamos capaces de identificar sus variables de estado, y las ecuaciones que las relacionan. Casi ná. Perdón, las variables de estado son las características fundamentales que describen al sistema. En el sistema simple del péndulo pueden ser la posición angular y la velocidad, por ejemplo. El número de variables necesarias determina el orden del sistema. A mayor orden, mayor número de variables y de ecuaciones. Más complejidad, vamos.
No confundir el estado del sistema con el sistema del Estado. Mientras el segundo puede ser neoliberal, marxista-lenilista y derivados, el primero es el valor de las variables de estado en un momento determinado. Suele ser útil representar el estado del sistema y su evolución en un gráfico muy mono y que quedan muy bien en cualquier trabajo o post bloguero, llamado espacio de estado. En él, cada variable es un eje de un sistema de coordenadas ortogonal. Vaya, ya metí un palabro, ejes perpendiculares de toda la vida, vamos.
Ea, ya estamos en condiciones de aproximarnos al concepto de atractor. Para ello, me serviré de un ejemplo de alto valor pedagógico que se me acaba de ocurrir en la ducha. Supongamos que nuestro espacio de estado es un bar (de Peter, por ejemplo). Nuestro sistema es el amigo Pasmao (el bloguero, no el personaje real), que acaba de entrar en el bar, y las variables de estado, las coordenadas de su posición dentro de nuestro bareto.
Bien, ¿cómo evolucionará nuestro sistema? Hay muchas posibilidades, entre ellas que el Pasmao reciba una llamada desde casa y salga disparado del bar nada más entrar (¡un sistema inestable!), pero veremos tres ejemplos de evolución hacia un atractor.
Opción A) El Pasmao ve una chica buenorra en el centro de la pista, y se tira flechado, sin más dilación, directamente. También vale si se acerca en espiral, lo mismo da. Una vez junto a ella, allí se queda pegado como un chicle bajo un pupitre: para siempre si nadie le echa. No os confundáis con mi ejemplo. Un atractor no es algo físico (la chica buenona), sino un punto o conjunto de puntos en el espacio de estado. En nuestro caso, el centro de la pista (donde he puesto a la chica buenona para que os pongáis en el lugar del Pasmao). Este tipo de atractor es un punto de equilibrio fijo.
Opción B) El Pasmao se queda dando vueltas alrededor de un grupo de pibas que está en la pista. Ahí se quedaría hasta siempre si no viene el novio de una de ellas para echarlo. La trayectoria que describe se denomina ciclo límite, y es otro tipo de atractor estable.
Opción C) El Pasmao se ha tomado más birras de la cuenta y se pone a dar bandazos de un lugar a otro de la pista de baile (no en la barra, ni en el patio, siempre en la pista), siguiendo trayectorias aparentemente aleatorias. Digo aparentemente, porque en realidad su marcha está dictada por unos misteriosos pasos de baile que sólo el sabe. Si dibujásemos su trayectoria después de varias horas, a lo mejor sale una linda mariposa, o un donut, o qué se yo. Esa zona de trayectorias posibles para nuestro amigo Pasmao, centradas en la pista de baile es un atractor extraño o atractor caótico.
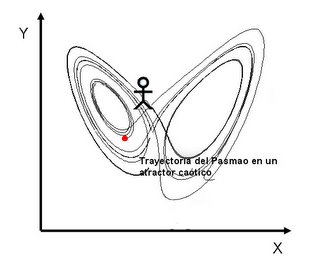
Quiero resaltar ahora que, aunque he tomado un ejemplo de espacio físico para que sea más fácil de asimilar, casi nunca es así. El espacio de estado es una representación mental de lo que está ocurriendo, ya que las variables de estado pueden ser magnitudes tales como la presión y la temperatura dentro de una olla donde se está cociendo un puchero, por ejemplo.
Otra consideración. Los sistemas dinámicos suelen dividirse en dos tipos: lineales y no lineales. Los primeros son aquellos en los que las alteraciones en su evolución son proporcionales a las alteraciones en su estado inicial. Dicho en cristiano: si le das el doble de candela a la olla, se calienta el doble el puchero. Sin embargo, la respuesta de los no lineales no siempre es proporcional.
Es fácil identificar un sistema no lineal a partir de sus ecuaciones de estado. Basta con comprobar si hay una variable multiplicada por otra, o elevada al cuadrado, o metida en un seno… Cualquier cosa que no sea del tipo ax’+by’+…=c, vamos.
¿Que para qué cuento todo esto? Porque el caos sólo puede aparecer en sistemas no lineales, por eso. En realidad, hay pocos sistemas totalmente lineales en la naturaleza, así que no os preocupéis. Ahora bien, no todos los sistemas no lineales pueden comportarse caóticamente.
Otra característica necesaria pero no suficiente para que aparezca el caos es el orden. Como mínimo, el sistema debe ser de orden 3, si no tiene excitación externa, o 2, si sí la tiene.
Creo que ya está bien por hoy. El próximo día, si aún hay alguien interesado, hablaremos sobre los fractales.
¡Ah!, se me olvidaba. En honor a Mizerable, aquí tenéis como ejemplo las ecuaciones de estado de un sistema caótico muy famoso en su casa: el de Lorenz.
x’=-ax+ay
y’=-xz+bx-y
z’=xy-cz
Este sistema tiene un atractor extraño en forma de mariposa (el del primer artículo) para a=10, b=28 y c=8/3.