Sobre el caos (III)

Cerraré esta pequeña serie de artículos sobre el caos hablando sobre fractales.
¿Qué es un fractal? La respuesta a esta pregunta es a la vez sencilla y compleja. Se conoce como fractal todo conjunto de puntos con una dimensión fraccionaria (fractional => fract-al).
Para explicarlo me apoyaré en los ejemplos que usa Lorenz en su libro “La esencia del caos”, ya referido con anterioridad. Los objetos comunes que conocemos tienen ninguna (un punto), una (una línea), dos (una superficie) o tres dimensiones (un sólido). Sin embargo, los matemáticos encontraron misteriosos conjuntos de puntos que carecían de algunas propiedades de los objetos de dimensión entera. Entonces redefinieron el concepto de dimensión y encontraron que dichos conjuntos de puntos tenían dimensión fraccionaria.
La dimensión se define a través del concepto de capacidad, que es el factor por el que tenemos que elevar a la base 2 para cubrir todos los puntos del conjunto a partir de sucesivas divisiones.
Así, en una superficie, al dividir un cuadrado en cuatro cuadrados, incrementamos el número de cuadrados necesarios en 2 elevado a 2. En una línea, sólo en 2 elevado a 1, ya que el número de cuadrados solamente se duplicará.
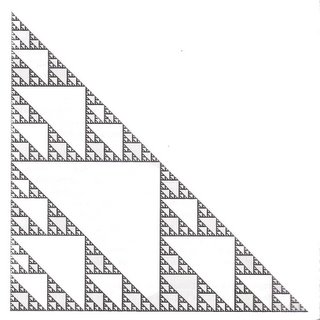
Sin embargo, imaginemos una figura tal que cada vez que dividimos en cuatro cuadrados, le quitamos el de la esquina superior derecha, por ejemplo. Al hacer el mismo cálculo, nos saldría una dimensión de
2^d=3
d= 1,586
La figura resultante se parecería a ésta
Pero los fractales no sólo existen en el campo teórico de las matemáticas, sino que los encontramos por doquier en la naturaleza. El ejemplo típico es el de una línea costera. ¿Qué longitud tiene? La respuesta es: depende. Si la medimos sobre un mapa, será menor que si la caminamos, ya que los pequeños cabos y entrantes de mar no aparecen el mapa. Y más grande le parecerá a una hormiguita que la recorra. Es decir, para encontrar la verdadera longitud de la costa hay que usar cuadraditos cada vez más pequeños. La dimensión entonces estará entre 1,0 y 2,0.
Una de las propiedades de los fractales puede verse claramente en el ejemplo de la primera figura: reproducen su estructura sea cual sea la escala a la que los observemos. Es lo que se denomina autosimilitud.

Las ramas de un árbol son otro ejemplo típico de una estructura fractal. Las ramas pequeñas reproducen la forma de las grandes. Lo mismo ocurre con los ríos o los capilares de nuestro sistema sanguíneo.
Pero nuestra intención era hablar del caos. ¿Cuál es la conexión? Pues que los atractores extraños, aquellos de los que hablamos en el artículo anterior, son objetos fractales. Por lo tanto, no todo lo fractal es caótico, pero sí todo lo que es caos tiene la propiedad de la fractalidad.
Por ejemplo, el atractor de Rossler, está compuesto por un conjunto apretado de líneas dobladas sobre sí mismas. No tiene dimensión 2 ni 3, sino algo intermedio.
Independientemente del valor científico del concepto, algunos fractales son objetos de gran belleza. A mi modesto entender, al menos.